Section1：入力層～中間層

1-1 要点

• 入力層: ニューラルネットワークに入力を受け取る箇所
• 中間層: 入力層から出力層までに入力と重みを掛け合わせたデータを受け取り、活性化関数を通じて次の中間層や出力層にデータを渡す箇所

数式で表すと以下のように表せる.

$$\boldsymbol{u} = \boldsymbol{W}\boldsymbol{x} + b$$ $$f(\boldsymbol{u})$$

• 入力: x
• 重み: w
• バイアス: b
• 中間層の総入力: u
• 中間層の出力: z
• 中間層の活性化関数: f

1-2 実装

# Google Colab での実行かを調べる
import sys
import os
ENV_COLAB = True  if 'google.colab' in sys.modules else False 

# google drive のマウント
if ENV_COLAB:
  from google.colab import drive 
  drive.mount('/content/drive')
  os.chdir('/content/drive/My Drive/rabitchallenge/Stage3/day1/DNN_code_colab_day1/notebook')

sys.path.append(os.pardir)

import numpy as np
from common import functions

def print_vec(text, vec):
    print("*** " + text + " ***")
    print(vec)
    print("shape: " + str(vec.shape))
    print("")

# 順伝播（単層・単ユニット）

# 重み
W = np.random.rand(2)
print_vec("重み", W)

# バイアス
b = np.random.rand() # 0~1のランダム数値
# print_vec("バイアス", b)  # floatにはshape関数がない

# 入力値
x = np.array([2, 3])
print_vec("入力", x)

# 総入力
u = np.dot(x, W) + b
print_vec("総入力", u)

# 中間層出力
z = functions.relu(u)
print_vec("中間層出力", z)

# 出力結果
*** 重み ***
[0.42432715 0.99087899]
shape: (2,)

*** 入力 ***
[2 3]
shape: (2,)

*** 総入力 ***
4.186902578605509
shape: ()

*** 中間層出力 ***
4.186902578605509
shape: ()

中間層の活性化関数にReLU関数を使っているため、\(u>0\)であることから総入力\(u\) = 中間層出力\(z\) となっている.

Section2 : 活性化関数

2-1 要点

• ニューラルネットワークにおいて、次の層の出力の大きさを決める非線形の関数.
• 入力値において次の層への信号のON/OFFや強度を決める働きを持つ.

中間層用の活性化関数

• ReLU関数
• シグモイド関数
• ステップ関数

出力層用の活性化関数

• ソフトマックス関数
• 恒等関数
• シグモイド関数

2-2 実装

活性化関数は以下のように記述される.

# 中間層の活性化関数
# シグモイド関数（ロジスティック関数）
def sigmoid(x):
    return 1/(1 + np.exp(-x))

# ReLU関数
def relu(x):
    return np.maximum(0, x)

# ステップ関数（閾値0）
def step_function(x):
    return np.where( x > 0, 1, 0) 

# 出力層の活性化関数
# ソフトマックス関数
def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T

    x = x - np.max(x) # オーバーフロー対策
    return np.exp(x) / np.sum(np.exp(x))

出力を見ると以下のようになる

def print_value(text, value):
    print("*** " + text + " ***")
    print(value)

x = 0.7

print_value("シグモイド関数", sigmoid(x));
print_value("ReLU関数", relu(x));
print_value("ステップ関数", step_function(x));

# 出力結果
*** シグモイド関数 ***
0.6681877721681662
*** ReLU関数 ***
0.7
*** ステップ関数 ***
1

Section3 : 出力層

3-1 要点

出力層の役割

人間が欲しいデータを出す必要がある.例えば分類問題であれば各クラスに属する確率など.

誤差関数

ニューラルネットワークの出力層で得られたデータと、正解データを比較することでどれくらいあっていたかを計算することができる.例えば二乗和誤差がある.

$$ \displaystyle E(w) = \frac{1}{2}\sum_{j=1}^J(y_j - d_j)^2 $$

• y: 正解データ
• d: 予測されたデータ

出力層の活性化関数

分類問題の場合、出力層の出力は0から1の範囲に限定し、総和を１となるような活性化関数を用いる.

各タスクで使用される関数が変わる.

• 回帰問題
  • 活性化関数: 恒等写像
  • 誤差関数: 二乗誤差
• 二値問題
  • 活性化関数: シグモイド関数
  • 誤差関数: 交差エントロピー
• 多クラス分類
  • 活性化関数: ソフトマックス関数
  • 誤差関数: 交差エントロピー

ソフトマックス関数 $$ \displaystyle f(i, u) = \frac{e^{u_i}}{\sum_{K=1}^Ke^{u_k}} $$ 交差エントロピー $$ E_n(w) = - \sum_{i_1}^Id_i\log{y_i} $$

3-2 実装

# 誤差関数
# 平均二乗誤差
def mean_squared_error(d, y):
    return np.mean(np.square(d - y)) / 2

# クロスエントロピー
def cross_entropy_error(d, y):
    if y.ndim == 1:
        d = d.reshape(1, d.size)
        y = y.reshape(1, y.size)

    # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
    if d.size == y.size:
        d = d.argmax(axis=1)

    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size

クロスエントロピーのreturn文にある 対数中の 1e-7は、マイナス無限大に対数の値がなって計算機で計算できなくならないようにするための工夫である.

Section4 : 勾配降下法

4-1 要点

ニューラルネットワークを学習する手法.

$$ w^{t+1} = w^t - ϵ∇E $$

• \(ϵ\): 学習率

学習率が大きすぎる場合発散する.一方で学習率が小さすぎる場合は収束するまでに時間がかかったり、誤差関数の極小値で学習が終わることがある.

収束性向上のためのアルゴリズム

以下のようなアルゴリズムがある.

• Momentum
• AdaGrad
• Adadelrta
• Adam

勾配降下法のバリエーション

• 確率的勾配降下法（SGD）

  • ランダムに抽出したサンプルの誤差を使う
  • メリット
    • データが冗長の場合の計算コスト軽減
    • 局所極小解に収束するリスクを抑える
    • オンライン学習ができる <-> バッチ学習

• ミニバッチ勾配降下法

  • ランダムに分割したデータの集合（ミニバッチ）$D_t$に属するサンプルの平均誤差
  • 一般的に使用されている手法.断りがなければ勾配降下法はミニバッチ勾配降下法をさす
  • メリット
    • 確率的勾配降下法のメリットを損なわず、計算機の計算資源を有効利用できる
      • CPUのスレッド並列化やGPUのSIMD並列化によって各ミニバッチを同時に計算できる

$$ \displaystyle E_t = \frac{1}{N_t} \sum_{n ∈ D_t} E_n $$

4-2 実装

import matplotlib.pyplot as plt

def f(x):
    y = 3 * x[0] + 2 * x[1]
    return y

# 初期設定
def init_network():
    network = {}
    nodesNum = 10
    network['W1'] = np.random.randn(2, nodesNum)
    network['W2'] = np.random.randn(nodesNum)
    network['b1'] = np.random.randn(nodesNum)
    network['b2'] = np.random.randn()

    return network

# 順伝播
def forward(network, x):    
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']
    u1 = np.dot(x, W1) + b1
    z1 = functions.relu(u1)
    
    u2 = np.dot(z1, W2) + b2
    y = u2
    
    return z1, y

# 誤差逆伝播
def backward(x, d, z1, y):
    grad = {}
    
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']

    # 出力層でのデルタ
    delta2 = functions.d_mean_squared_error(d, y)
    # b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)
    # W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)
    # 中間層でのデルタ
    delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)

    delta1 = delta1[np.newaxis, :]
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    x = x[np.newaxis, :]
    # W1の勾配
    grad['W1'] = np.dot(x.T, delta1)

    return grad

# サンプルデータを作成
data_sets_size = 100000
data_sets = [0 for i in range(data_sets_size)]

for i in range(data_sets_size):
    data_sets[i] = {}
    # ランダムな値を設定
    data_sets[i]['x'] = np.random.rand(2)
    # 目標出力を設定
    data_sets[i]['d'] = f(data_sets[i]['x'])
    
losses = []
# 学習率
learning_rate = 0.07

# 抽出数
epoch = 100

# パラメータの初期化
network = init_network()
# データのランダム抽出
random_datasets = np.random.choice(data_sets, epoch)

# 勾配降下の繰り返し
for dataset in random_datasets:
    x, d = dataset['x'], dataset['d']
    z1, y = forward(network, x)
    grad = backward(x, d, z1, y)
    # パラメータに勾配適用
    for key in ('W1', 'W2', 'b1', 'b2'):
        network[key]  -= learning_rate * grad[key]

    # 誤差
    loss = functions.mean_squared_error(d, y)
    losses.append(loss)

print("##### 結果表示 #####")    
lists = range(epoch)

plt.plot(lists, losses)
# グラフの表示
plt.show()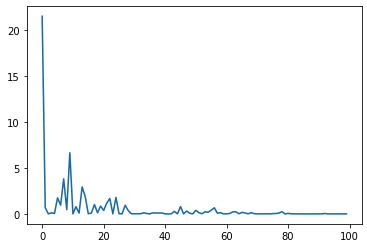

# 勾配降下の繰り返しの箇所で、入力データと正解データのデータセットを１つづつ抜き出して、勾配を計算しているため確率的勾配降下法となっている.

Section5 : 誤差逆伝播法

5-1 要点

算出された誤差を、出力層側から順に微分して、前の層、前の層へと伝播して計算する.
微分の連鎖律を用いて、最小限の計算で各パラメータでの微分値を解析的に計算することができる.
ノードのグラフを見ながら出力層から順繰りに遡って微分値を計算していけばよい.

5-2 実装

誤差逆伝播の実装は4-2 実装で行っている. 誤差逆伝播の関数は、backward(x, d, z1, y)で定義され、勾配降下を繰り返している学習中にその関数呼ばれて計算をしている.