Section1：再帰型ニューラルネットワークの概念

1-1 要点

RNN

時系列データを扱えるニューラルネットワークである.

時系列データの例

• 音声データ
• 株価データ

RNNの数学的記述

• $u^t = W_{(in)}x^t+ZWz^{t-1}+b$: 中間層に入る前.入力と、前の時刻の中間層からの入力と、バイアス .
• $z^t = f(u^t)$: 中間層の状態. 活性化関数を通した$u^t$
• $v^t = W_{out}z^t+c$: 出力層の活性化関数を通る前.
• $y^t = g(v^t)$ 出力層. 活性化関数を通した$v^t$

BPTT

BPTT: Backpropagation Through Time

BPTTの数学的記述

• $\displaystyle \frac{∂E}{∂W_{(in)}} = \frac{∂E}{∂u^t}\left[\frac{∂u^t}{∂W_{(in)}}\right]^T = δ^t[x^t]^T$
  • $δ^t$は、$\displaystyle \frac{∂E}{∂u^t}$を計算したもの.
  • $\displaystyle \frac{∂u^t}{∂W_{(in)}} = \frac{∂(W_{(in)}x^t+ZWz^{t-1}+b)}{∂W_{(in)}} = x^t$のように計算できる.
• $\displaystyle \frac{∂E}{∂W_{(out)}} = \frac{∂E}{∂v^t}\left[\frac{∂v^t}{∂W_{(out)}}\right]^T = δ^{out,t}[z^t]^T$
• $\displaystyle \frac{∂E}{∂W} = \frac{∂E}{∂u^t}\left[\frac{∂u^t}{∂W}\right]^T = δ^t[z^{t-1}]^T$
• $\displaystyle \frac{∂E}{∂b} = \frac{∂E}{∂u^t}\frac{∂u^t}{∂b} = δ^t$
• $\displaystyle \frac{∂E}{∂c} = \frac{∂E}{∂v^t}\frac{∂v^t}{∂c} = δ^{out,t}$

1-2 実装

import sys
import os
ENV_COLAB = True  if 'google.colab' in sys.modules else False 

# google drive のマウント
if ENV_COLAB:
  from google.colab import drive 
  drive.mount('/content/drive')
  os.chdir('/content/drive/My Drive/rabitchallenge/Stage3/day3/DNN_code_colab_day3/notebook')

sys.path.append(os.pardir) 

import numpy as np
from common import functions
import matplotlib.pyplot as plt

# [try] 中間層の活性化関数を変更してみよう 導関数をd_tanhとして作成しよう
def d_tanh(x):
    return 4 / (np.exp(x) + np.exp(-x))**2

# データを用意
# 2進数の桁数
binary_dim = 8
# 最大値 + 1
largest_number = pow(2, binary_dim)
# largest_numberまで2進数を用意
binary = np.unpackbits(np.array([range(largest_number)],dtype=np.uint8).T,axis=1)

# [try] weight_init_stdやlearning_rate, hidden_layer_sizeを変更してみよう
input_layer_size = 2  
hidden_layer_size = 16
output_layer_size = 1

weight_init_std = 1
learning_rate = 0.2  # 0.1から変更

iters_num = 10000
plot_interval = 100

# ウェイト初期化 (バイアスは簡単のため省略)
# Xavier [try] 重みの初期化方法を変更してみよう
def weight_init_std_xavier(layer_size):
    return np.sqrt(1.0 / layer_size)

W_in = weight_init_std * np.random.randn(input_layer_size, hidden_layer_size)
W_out = weight_init_std_xavier(hidden_layer_size) * np.random.randn(hidden_layer_size, output_layer_size)
W = weight_init_std_xavier(input_layer_size) * np.random.randn(hidden_layer_size, hidden_layer_size)

# 勾配
W_in_grad = np.zeros_like(W_in)
W_out_grad = np.zeros_like(W_out)
W_grad = np.zeros_like(W)

u = np.zeros((hidden_layer_size, binary_dim + 1))
z = np.zeros((hidden_layer_size, binary_dim + 1))
y = np.zeros((output_layer_size, binary_dim))

delta_out = np.zeros((output_layer_size, binary_dim))
delta = np.zeros((hidden_layer_size, binary_dim + 1))

all_losses = []

for i in range(iters_num):
    
    # A, B初期化 (a + b = d)
    a_int = np.random.randint(largest_number/2)
    a_bin = binary[a_int] # binary encoding
    b_int = np.random.randint(largest_number/2)
    b_bin = binary[b_int] # binary encoding
    
    # 正解データ
    d_int = a_int + b_int
    d_bin = binary[d_int]
    
    # 出力バイナリ
    out_bin = np.zeros_like(d_bin)
    
    # 時系列全体の誤差
    all_loss = 0    
    
    # 時系列ループ
    for t in range(binary_dim):
        # 入力値
        X = np.array([a_bin[ - t - 1], b_bin[ - t - 1]]).reshape(1, -1)
        # 時刻tにおける正解データ
        dd = np.array([d_bin[binary_dim - t - 1]])
        
        u[:,t+1] = np.dot(X, W_in) + np.dot(z[:,t].reshape(1, -1), W)
        #z[:,t+1] = functions.sigmoid(u[:,t+1])
        # [try] 中間層の活性化関数を変更してみよう reluに変更
        #  -> 学習が進んでいないことが確認できた
        #z[:,t+1] = functions.relu(u[:,t+1])
        # [try] 中間層の活性化関数を変更してみよう tanhに変更
        z[:,t+1] = np.tanh(u[:,t+1])

        y[:,t] = functions.sigmoid(np.dot(z[:,t+1].reshape(1, -1), W_out))

        #誤差
        loss = functions.mean_squared_error(dd, y[:,t])
        #delta_out[:,t] = functions.d_mean_squared_error(dd, y[:,t]) * functions.d_sigmoid(y[:,t])
        # [try] 中間層の活性化関数を変更してみよう reluに変更 -> 逆伝播の計算にはd_reluを使う 
        #  -> 学習が進んでいないことが確認できた
        #delta_out[:,t] = functions.d_mean_squared_error(dd, y[:,t]) * functions.d_relu(y[:,t])
        # [try] 中間層の活性化関数を変更してみよう tanhに変更 -> 逆伝播の計算にはd_tanhを使う
        delta_out[:,t] = functions.d_mean_squared_error(dd, y[:,t]) * d_tanh(y[:,t])        

        all_loss += loss

        out_bin[binary_dim - t - 1] = np.round(y[:,t])
    
    
    for t in range(binary_dim)[::-1]:
        X = np.array([a_bin[-t-1],b_bin[-t-1]]).reshape(1, -1)        

        delta[:,t] = (np.dot(delta[:,t+1].T, W.T) + np.dot(delta_out[:,t].T, W_out.T)) * functions.d_sigmoid(u[:,t+1])

        # 勾配更新
        W_out_grad += np.dot(z[:,t+1].reshape(-1,1), delta_out[:,t].reshape(-1,1))
        W_grad += np.dot(z[:,t].reshape(-1,1), delta[:,t].reshape(1,-1))
        W_in_grad += np.dot(X.T, delta[:,t].reshape(1,-1))
    
    # 勾配適用
    W_in -= learning_rate * W_in_grad
    W_out -= learning_rate * W_out_grad
    W -= learning_rate * W_grad
    
    W_in_grad *= 0
    W_out_grad *= 0
    W_grad *= 0
    
    # レポート上は途中経過の出力を抑止
    if(i % plot_interval == 0):
        all_losses.append(all_loss)        
        #print("iters:" + str(i))
        #print("Loss:" + str(all_loss))
        #print("Pred:" + str(out_bin))
        #print("True:" + str(d_bin))
        out_int = 0
        for index,x in enumerate(reversed(out_bin)):
            out_int += x * pow(2, index)
        #print(str(a_int) + " + " + str(b_int) + " = " + str(out_int))
        #print("------------")

lists = range(0, iters_num, plot_interval)
plt.plot(lists, all_losses, label="loss")
plt.show()

中間層の活性化関数をsigmoidからreluに変更すると勾配爆発が起こり学習が進まないことがわかった.また、tanhに変更すると学習は進むものの、収束はしなかった. 他のパラメータは同じでも中間層の活性化関数の選び方で結果は変わってくる.

1-3 関連学習

tanhの導関数は以下のような数式になる. $$ \tanh^\prime = \frac{4}{(e^x + e^{-x})^2} = \frac{1}{(\cosh x)^2} $$ またnumpyにはcosh関数が用意されている.

https://numpy.org/doc/stable/reference/generated/numpy.cosh.html

Section2：LSTM

2-1 要点

RNNの課題

• 時系列を遡るほど、勾配消失が起こる.

RNNの課題を解決するためにニューラルネットワークを改良して、LSTMが考案された.

CEC

RNNでは学習と記憶を同時に行っていた.LSTMでは学習と記憶を分離して、CECに’記憶’のみを担うようにしている.

入力ゲートと出力ゲート

入力ゲートは今回の入力値と前回の出力値をどれだけ使ってCECに値を渡すかを学習する 出力ゲートは今回の入力値と前回の出力値をどれだけ使ってCECの値を使うかを学習する

忘却ゲート

CECは過去の情報を保持し続けてしまうため忘却ゲートを設けてCECの値に作用させる

覗き穴結合

CECの値も使って入力ゲート、忘却ゲート、出力ゲートを更新しようという試み.

2-2 実装

# 実装演習ソースコードがないため、演習チャレンジからlstmの実装を記載
def lstm(x, prev_h, prev_c, W, U, b):
  # セルへの入力やゲートをまとめて計算し、分割
  lstm_in = _activation(x.dot(W.T)) + prev_h.dot(U.T) + b)
  a, i, f, o = np.hsplit(lstm_in, 4)

  a = np.tanh(a)
  input_gate = _sigmoid(i)
  forget_gate = _sigmoid(f)
  output_gate = _sigmoid(o)

  # セルの状態を更新し、中間層の出力を計算
  # ↓CECは入力ゲートと忘却ゲートから更新を受けている
  c = input_gate * a + forget_gate * c 
  h = output_gate * np.tanh(c)
  return c, h

2-3 関連学習

LSTMは「入力ゲートと忘却ゲートで短期と長期の情報のバランスを調整してセルの値を更新している」 （「深層学習による自然言語処理」p.35より）

RNNでは前回の入力値（短期の記憶）の情報を学習してしまう傾向にあるため、CECという記憶用のセルが用意されたり、ゲートを加えることで前回出力層からの入力以外の入力を使用したりしているようだ.

Section3：GRU

3-1 要点

LSTMではパラメータが多く計算負荷が大きかった.GRUはパラメータ量を減らし、LSTMの精度と同等かそれ以上になったニューラルネットワークモデル.

GRU（Gated Recurrent Unit）には２つのゲートがある.

• リセットゲート
• 更新ゲート

3-2 実装

# 実装演習ソースコードがないため、演習チャレンジから実装を記載
def gru(x, h, W_r, U_r, W_z, U_z, W, U):
  # ゲートを計算
  # ↓リセットゲート
  r = _sigmoid(x.dot(W_r.T) + h.dot(U_r.T)) 
  # ↓更新ゲート
  z = _sigmoid(x.dot(W_z.T) + h.dot(U_z.T)) 

  # 次の状態を計算
  h_bar = np.tanh(x.dot(W.T) + (r * h).dot(U.T)) 
  h_new = (1-z) * h + z * h_bar  
  return h_new

3-3 関連学習

「GRUはLSTMよりゲートが少なくセルも必要ないため、状態変数の数が同じであればLSTMより少ない計算量・使用空間量で済みます」 （「深層学習による自然言語処理」p.36より）

講義動画中にも述べられていたが、LSTMのようなRNNに比べれば少し複雑になったと思えるニューラルネットも似たような機構でより少ないパラメータにできないかを考えてGRUが生まれたそうだ.

ニューラルネットワークの構造・機構のエッセンスが何かを意識しながら、既存のモデルとの差異を理解していくことが大事に思えた.

Section4：双方向RNN

4-1 要点

過去の情報だけでなく、未来の情報を加味することで制度を向上させるためのモデル. 例えば文章だと過去（以前の単語・文章）と未来（次の単語・文章）どちらもアクセスできる.

実用例として、文章の推敲や機械翻訳がある.

4-2 実装

# 実装演習ソースコードがないため、演習チャレンジから実装を記載
def bidirectional_rnn_net(xs, W_f, U_f, W_b, U_b, V):
  # W_f, U_f： 順方向の重み
  # W_b, U_b： 逆方向の重み
  # V： 重み
  xs_f = np.zeros_like(xs)
  xs_b = np.zeros_like(xs)

  for i, x in enumerate(xs):
    xs_f[i] = x
    xs_b[i] = x[::-1]

  hs_f = _rnn(xs_f, W_f, U_f)
  hs_b = _rnn(xs_b, W_b, U_b)
  # ↓足したりかけたりすると特徴量の意味が変わってしまうためconcatenateでベクトルをまとめる
  hs = [np.concatenate([h_f, h_b[::-1]], axis=1)] for h_f, h_b in zip(hs_f, hs_b)]
  ys = hs.dot(V.T)
  return ys

Section5：Seq2Seq

5-1 要点

Encoder-Decoderモデルの一種.機械翻訳であればエンコーダーで文脈を理解し、デコーダーで新たな文を生成する.

Encoder RNN

MLM: Masked Language Model

Decoder RNN

1. Encoder RNNのfinal state(thought vector)から、各トークンの生成確率を出力する final stateをDecoder RNNのinitial stateとして設定しEmbeddingを入力する
2. Sampling: 生成確率に基づいてtokenをランダムに選ぶ
3. Embeding: 2で選ばれたtokenをEmbeddingしてDocoder RNNの次の入力とする
4. Detokednize: 1-3を繰り返して2で得られたトークンを文字列に直す

HRED

Seq2Seqは一文一答型だったので、文脈を含めて文を生成するモデルが考案された

HRED = Seq2Seq + Context RNN

でも、短い応答しかしなくなるという課題が発生した.

VHRED

HREDの課題をVAEの潜在変数の概念を導入したもの.

VAE

オートエンコーダ

教師なし学習の一つ. 入力をエンコーダを潜在変数zを計算し、潜在変数zからデコーダを通じて入力と同じ出力になるように学習する.

VAE: Variational AutoEncoder

潜在変数zに平均0分散1である確率分布を仮定したもの.

5-2 実装

# 演習チャレンジから実装を記載
def encode(words, E, W, U, b):
  # words： one-hotベクトルで表現された文にある単語たち
  # E：単語の埋め込み行列
  # W：重み
  # U：重み
  # b：バイアス
  hidden_size = W.shape[0]
  h = np.zeros(hidden_size)

  for w in words:
    # ↓埋め込み行列と単語のone-hotベクトルの内積を取ることで単語の埋め込み表現が取り出せる
    e = E.dot(w) 
    h = _activation(W.dot(e) + U.dot(h) + b)
  return h

Section6：Word2vec

6-1 要点

単語をベクトル表現する手法. 単語をone-hotベクトルにしたあと、単語をembeddingしたベクトルで表すように学習するもの.

単語のembedding表現ができると、単語をone-hotベクトルよりも少ない数値で表せるようになり、少ないデータで単語の分散表現を得ることができる.

そのため計算量が少なくて済み、計算機で扱いやすくなった.

6-2 実装

# 3_11_nlp-basic.ipynbより一部抜粋

import spacy
import numpy as np

# word2vecの処理が行われたライブラリを使用している
nlp = spacy.load('ja_ginza')  # <- 自然言語ライブラリを読み込む 参考: https://www.koi.mashykom.com/spacy_ginza.html
target2index = pd.get_dummies(targets)

def get_features_and_labels_for_spacy(original_df):
  features = []
  labels = []
  max_feature_len = 0
  for i, original in enumerate(original_df.iterrows()):
    sentence = original[1]['sentence']
    target = original[1]['target']

    doc = nlp(sentence)   # <- nlpに文章を与えると形態素解析が行われる
    feature = [token.vector for token in doc]
    max_feature_len = max(max_feature_len, len(feature))
    label = target2index[target].values

    features.append(feature)
    labels.append(label)

  return np.asarray(features), np.asarray(labels), max_feature_len

Section7：Attention Mechanism

7-1 要点

seq2seqでは長い文章への対応が難しかったことへの対処としてAttention Mechanismが考案された.. 時系列データの中身に関連性に重みをつける手法. 例えば I have a pen.の日本語訳にはaはそれほど重要でないと学習する.

近年の自然言語処理では一般的にAttention Mechanismが使用されている.

7-2 実装

演習コードがないため割愛.

7-3 関連学習

Attention Mechanism: 注意機構にはソフト注意機構とハード注意機構がある.（その他の注意機構もある）

複数のベクトルがあったとき、どのベクトルを重要視するか含めて学習させる仕組みのことを注意機構という.

• ソフト注意機構
  • 複数ベクトルの重み付き平均を使う手法
• ハード注意機構
  • 複数ベクトルから確率的に1つに選択する手法

（「深層学習による自然言語処理」 p.91 chapter4 言語処理特有の深層学習の発展 を参照）

8: VQ-VAE

8-1 要点

VAEの派生の生成モデル.

• VAE: 潜在変数zがガウス分布に従うベクトルになるように学習を行う
• VQ-VAE: 潜在変数zが離散的な数値になるように学習を行う

離散的な潜在変数にするメリット

• 離散変数の方がデータの特徴を捉えられる.
  • 例えば画像認識で「車」や「猫」という言葉で表現できる.言葉は離散的な表現であり、より簡潔にデータの特徴を捉えられそう
• posterior collapseを防げる
  • VAEで画像生成するとき、デコーダを通して得たデータの輪郭はぼやけることが多い.離散的な値を使うとそれが防げるらしい

9: [フレームワーク演習] 双方向RNN / 勾配のクリッピング

9-1 要点

• 実装にはspoken digit datasetを使用する. MNISTの音声版となっている
• 音声データの長さを揃えてから学習に使用する
  • データが短いものはパディングを行う
• 音声データは波形としてみることができる
• map関数を使ってデータ１つ１つを取り出して加工することができる

9-2 実装

!pip install pydub
import tensorflow_datasets as tfds
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf

dataset_train, dataset_valid, dataset_test = tfds.load('spoken_digit', split=['train[:70%]', 'train[70%:85%]', 'train[85%:]'], shuffle_files=True)

original_iter = iter(dataset_train)

# 波形確認
plt.plot(next(original_iter)['audio'])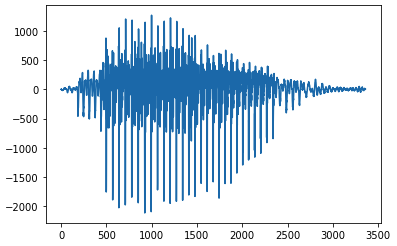

# データの前処理
NUM_DATA_POINTS = 1000
BATCH_SIZE = 8

def cut_if_longer(el):
  return (
          tf.reshape(
              tf.cond(
                tf.greater(tf.shape(el['audio']), NUM_DATA_POINTS),
                true_fn=lambda: tf.slice(el['audio'], begin=[0], size=[NUM_DATA_POINTS]),
                false_fn=lambda: tf.slice(tf.concat([el['audio'], tf.zeros(NUM_DATA_POINTS, tf.int64)], axis=0), begin=[0], size=[NUM_DATA_POINTS])
              ),
              shape=(-1, 1)
          ),
          [el['label']]
        )


dataset_prep_train = dataset_train.map(cut_if_longer).batch(BATCH_SIZE)
dataset_prep_valid = dataset_valid.map(cut_if_longer).batch(BATCH_SIZE)

sample = next(iter(dataset_prep_valid))

# 双方向RNN(LSTM)を使用したモデル
from tensorflow.keras.models import Sequential
from tensorflow.keras import layers

tf.keras.backend.clear_session()

model_4 = tf.keras.models.Sequential()
model_4.add(layers.Input((NUM_DATA_POINTS, 1)))
model_4.add(layers.Bidirectional(layers.LSTM(64)))
model_4.add(layers.Dense(10, activation='softmax'))

model_4.summary()  # <- モデルの確認をおこなっている
model_4.predict(sample[0]).shape

model_4.compile(
    loss=tf.keras.losses.SparseCategoricalCrossentropy(),
    optimizer=tf.keras.optimizers.Adam(clipvalue=0.5), # <- 勾配のクリッピングはoptimizerに指定
    metrics=['accuracy']
)

model_4.fit(
    dataset_prep_train,
    validation_data=dataset_prep_valid,
)

# 出力結果
Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 bidirectional (Bidirectiona  (None, 128)              33792     
 l)                                                              
                                                                 
 dense (Dense)               (None, 10)                1290      
                                                                 
=================================================================
Total params: 35,082
Trainable params: 35,082
Non-trainable params: 0
_________________________________________________________________
219/219 [==============================] - 161s 715ms/step - loss: 2.2837 - accuracy: 0.1434 - val_loss: 2.1733 - val_accuracy: 0.1920
<keras.callbacks.History at 0x7fa7c549a8d0>

10: [フレームワーク演習] Seq2Seq

10-1 要点

• Seq2Seq(Encoder-Decoder)モデルを用いたsin-cosの変換を行う.
• エンコーダーの出力であるstateをデコーダーの入力として使用している
• state以外はエンコーダーとデコーダーは独立したニューラルネットワークモデルとして作成されている

10-2 実装

Seq2Seq(Encoder-Decoder) の実行

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-3 * np.pi, 3 * np.pi, 100)
seq_in = np.sin(x)
seq_out = np.cos(x)

# NUM_ENC_TOKENS: 入力データの次元数
# NUM_DEC_TOKENS: 出力データの次元数
# NUM_HIDDEN_PARAMS: 単純RNN層の出力次元数(コンテキストの次元数にもなる)
# NUM_STEPS: モデルへ入力するデータの時間的なステップ数。

NUM_ENC_TOKENS = 1
NUM_DEC_TOKENS = 1
NUM_HIDDEN_PARAMS = 10
NUM_STEPS = 24

# 学習のモデル定義を行う

tf.keras.backend.clear_session()

e_input = tf.keras.layers.Input(shape=(NUM_STEPS, NUM_ENC_TOKENS), name='e_input')
_, e_state = tf.keras.layers.SimpleRNN(NUM_HIDDEN_PARAMS, return_state=True, name='e_rnn')(e_input)

d_input = tf.keras.layers.Input(shape=(NUM_STEPS, NUM_DEC_TOKENS), name='d_input')
d_rnn = tf.keras.layers.SimpleRNN(NUM_HIDDEN_PARAMS, return_sequences=True, return_state=True, name='d_rnn')
d_rnn_out, _ = d_rnn(d_input, initial_state=[e_state])

d_dense = tf.keras.layers.Dense(NUM_DEC_TOKENS, activation='linear', name='d_output')
d_output = d_dense(d_rnn_out)

model_train = tf.keras.models.Model(inputs=[e_input, d_input], outputs=d_output)
model_train.compile(optimizer='adam', loss='mean_squared_error')

model_train.summary()

# 学習用データの準備
n = len(x) - NUM_STEPS
ex = np.zeros((n, NUM_STEPS))
dx = np.zeros((n, NUM_STEPS))
dy = np.zeros((n, NUM_STEPS))

for i in range(0, n):
  ex[i] = seq_in[i:i + NUM_STEPS]
  dx[i, 1:] = seq_out[i:i + NUM_STEPS - 1]
  dy[i] = seq_out[i: i + NUM_STEPS]

ex = ex.reshape(n, NUM_STEPS, 1)
dx = dx.reshape(n, NUM_STEPS, 1)
dy = dy.reshape(n, NUM_STEPS, 1)

# 学習の実行
BATCH_SIZE = 16
EPOCHS = 80

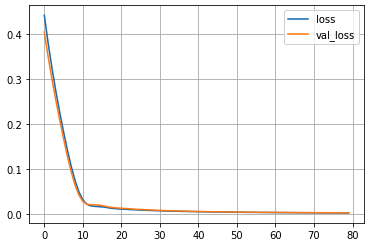
history = model_train.fit([ex, dx], dy, batch_size=BATCH_SIZE, epochs=EPOCHS, validation_split=0.2, verbose=False)

loss = history.history['loss']
plt.plot(np.arange(len(loss)), loss, label='loss')

loss = history.history['val_loss']
plt.plot(np.arange(len(loss)), loss, label='val_loss')

plt.grid()
plt.legend()
plt.show()

# 出力結果
Model: "model"
__________________________________________________________________________________________________
 Layer (type)                   Output Shape         Param #     Connected to                     
==================================================================================================
 e_input (InputLayer)           [(None, 24, 1)]      0           []                               
                                                                                                  
 d_input (InputLayer)           [(None, 24, 1)]      0           []                               
                                                                                                  
 e_rnn (SimpleRNN)              [(None, 10),         120         ['e_input[0][0]']                
                                 (None, 10)]                                                      
                                                                                                  
 d_rnn (SimpleRNN)              [(None, 24, 10),     120         ['d_input[0][0]',                
                                 (None, 10)]                      'e_rnn[0][1]']                  
                                                                                                  
 d_output (Dense)               (None, 24, 1)        11          ['d_rnn[0][0]']                  
                                                                                                  
==================================================================================================
Total params: 251
Trainable params: 251
Non-trainable params: 0
__________________________________________________________________________________________________

# 推論の準備
model_pred_e = tf.keras.models.Model(inputs=[e_input], outputs=[e_state])
pred_d_input = tf.keras.layers.Input(shape=(1, 1))
pred_d_state_in = tf.keras.layers.Input(shape=(NUM_HIDDEN_PARAMS))
pred_d_output, pred_d_state = d_rnn(pred_d_input, initial_state=[pred_d_state_in])
pred_d_output = d_dense(pred_d_output)
pred_d_model = tf.keras.Model(inputs=[pred_d_input, pred_d_state_in], outputs=[pred_d_output, pred_d_state])

def predict(input_data):
  state_value = model_pred_e.predict(input_data)
  _dy = np.zeros((1, 1, 1))
  
  output_data = []
  for i in range(0, NUM_STEPS):
    # <- エンコーダーのstate_valueを受け取ってデコーダーで予測を行う
    y_output, state_value = pred_d_model.predict([_dy, state_value]) 
    
    output_data.append(y_output[0, 0, 0])
    _dy[0, 0, 0] = y_output

  return output_data

# 推論を行う
init_points = [0, 24, 49, 74]

for i in init_points:
  _x = ex[i : i + 1]
  _y = predict(_x)
    
  if i == 0:
    plt.plot(x[i : i + NUM_STEPS], _y, color="red", label='output')
  else:
    plt.plot(x[i : i + NUM_STEPS], _y, color="red")

plt.plot(x, seq_out, color = 'blue', linestyle = "dashed", label = 'correct')
plt.grid()
plt.legend()
plt.show()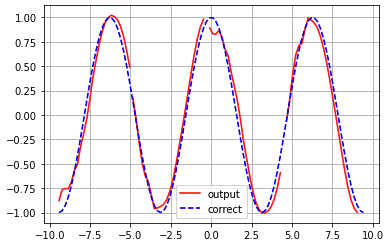 

11: [フレームワーク演習] data-augumentation

11-1 要点

data-augumentationはデータの水増しのこと. 画像の場合は、手元にあるデータから擬似的に別の画像を生成して学習データに使うことで画像認識制度を上げる.具体的な水増し手法には主に以下があり、それらを組み合わせて使用する.

• 反転: Horizontal Flip, Vertical Flip
• 回転: Rotate
• 変形: Random Erasing, Mixup
• 切り出し: Crop
• 加工: Contrast, Brightness, Hue（色相)

11-2 実装

import numpy as np
import tensorflow as tf
import random
import matplotlib.pyplot as plt

def show_images(images):
    """複数の画像を表示する"""
    n = 1
    while n ** 2 < len(images):
        n += 1
    for i, image in enumerate(images):
        plt.subplot(n, n, i + 1)
        plt.imshow(image)
        plt.axis('off')
    plt.show()

! mkdir sample_data
! wget -qnc --no-check-certificate -O ./sample_data/image_origin.jpg \
https://github.com/opencv/opencv/raw/master/samples/data/fruits.jpg

contents = tf.io.read_file("./sample_data/image_origin.jpg")
image_origin = tf.image.decode_jpeg(contents, channels=3)

image = image_origin
show_images([image.numpy()])

# 複数の手法を組み合わせる
def data_augmentation(image):
    image = tf.image.random_flip_left_right(image)  # <- 左右反転
    image = tf.image.random_flip_up_down(image)  # <- 上下反転
    image = tf.image.random_contrast(image, lower=0.4, upper=0.6)  # <- コントラスト変更
    image = tf.image.random_brightness(image, max_delta=0.8)  # <- 輝度変更
    image = tf.image.rot90(image, k=random.choice((0, 1, 2)))  # <- 0度, 90, 180度回転
    image = tf.image.random_hue(image, max_delta=0.1)  # <- 色相変更
    return image

image = image_origin

show_images([data_augmentation(image).numpy() for _ in range(36)])

12: [フレームワーク演習] activate_functions

12-1 要点

• 関数（=函数）とは変換器のこと. 函数の函は箱の意味.
• 活性化関数
  • 誤差逆伝播法で計算するために活性化関数と活性化関数の導関数が必要となる

さまざまな活性化関数

中間層で使用される活性化関数

• ステップ関数
• シグモイド関数
• ハイパボリックタンジェント関数
• ReLU: 正規化線形関数
  • 勾配消失が発生しにくいため現在主流の関数
  • 導関数の入力値が負になると値が0になり学習が進まない
• Leakey ReLU
  • 導関数の入力値が負の場合値α=0.01を用いて学習を進められるようにしている
• Swish
  • ReLUの代替として使用される
  • なめらかなReLUのようなグラフ形状. シグモイド関数が含まれている

出力層で使用される活性化関数

• シグモイド関数
• ソフトマックス関数
  • 多クラス分類で使用される
• 恒等関数

12-2 実装

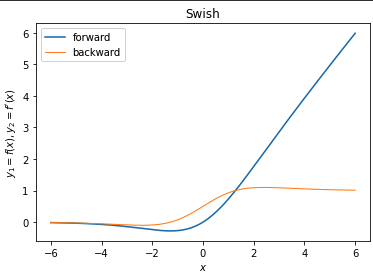
# Swishを実装する
beta = 1.0
def sigmoid(x):
    return 1.0 / (1.0 + np.exp(-x))

def swish(x):
    """forward
       
       Swish
       シグモイド加重線形関数
    """
    return x * sigmoid(beta*x)

def d_swish(x):
    """backward
       
       derivative of Swish
       シグモイド加重線形関数の導関数
    """
    dx = beta*swish(x) + sigmoid(beta*x)*(1.0 - beta*swish(x)) 
    return dx

x = np.arange(-600, 601, 1) * 0.01
f, d = swish, d_swish
y1, y2 = f(x), d(x)

_, ax = plt.subplots()
# label=を見ると関数のコメントの箇所から"forward", "backward"を抜き出していることがわかる
ax.plot(x, y1, label=f.__doc__.split("\n")[0].strip())
ax.plot(x, y2, label=d.__doc__.split("\n")[0].strip(), linewidth=1.0) 
ax.set_xlabel("$x$")
ax.set_ylabel("$y_{1}=f(x), y_{2}=f^{\prime}(x)$") 
ax.set_title(f.__doc__.split("\n")[2].strip())   # <- 関数のコメントの箇所から"Swish"を抜き出す
ax.legend()

plt.show()