線形回帰モデル

要点

回帰問題

回帰問題はある入力から出力を予測する問題

直線で予測 -> 線形回帰
曲線で予測 -> 非線形回帰

回帰で扱うデータ

入力：　各要素を説明変数、特徴量
出力: 目的変数

線形回帰モデル

線形回帰モデルは、回帰問題を解くための機械学習モデルの１つ。

$$ \hat y = \boldsymbol{w^\top}\boldsymbol{x} + w_0 = \sum_{j=1}^mw_jx_j + w_0$$

パラメータwは未知。

説明変数が1次元の場合

$$ y = w_0 + w_1x_1 + ε$$

y: 目的変数（既知）
w_0: 切片（未知: 学習で決める）
w_1: 回帰係数（未知: 学習で決める）
x_1: 説明変数（既知: 入力データ）
ε: 誤差. 偶発誤差や、x_1以外の影響

説明変数が多次元の場合

n個の連立方程式を考える。連立方程式は行列で表せる。

$$ \boldsymbol{y} = \boldsymbol{X}\boldsymbol{w} $$

$\boldsymbol{X}$: 計画行列と呼ぶ。

具体的には下記のように表せる。

$$ \left( \begin{array}{c} y_1 \ y_2 \ \vdots \ y_n \end{array} \right) = \left( \begin{array}{cccc} 1 & x_{11} & \ldots & x_{1m} \ 1 & x_{21} & \ldots & x_{2m} \ \vdots & \vdots & \ddots & \vdots \ 1 & x_{n1} & \ldots & x_{nm} \end{array} \right) \left( \begin{array}{c} w_1 \ w_2 \ \vdots \ w_m \end{array} \right) $$

$\boldsymbol{y}$ : $n \times 1$ 行列
$\boldsymbol{X}$ : $n \times (m+1)$ 行列
$\boldsymbol{w}$ : $(m+1) \times 1$ 行列

留意点

Xの列の次元数とwの行の次元数は一致してないと内積計算できない。
連立方程式を解くには、変数以上の方程式がないと解けない。
- パラメータ数よりも多いデータが必要なため、ディープラーニングでは多数のデータが必要となる。

二乗誤差

$$ \sum_i(\hat{y_i} - y_i)^2 $$

二乗損失は一般に外れ値に弱い
- 二乗損失を使う場合はまずは外れ値がないかを確認すること。
- Huber損失やTukey損失を使うことがある

実装

設定

ボストンの住宅データセットを線形回帰モデルで分析する

課題

部屋数が4で犯罪率が0.3の物件はいくらになるか？

# モジュールとデータのインポート
from sklearn.datasets import load_boston
from pandas import DataFrame
import numpy as np
from sklearn.linear_model import LinearRegression

# bostonというインスタンスにインポート
boston = load_boston()

# 説明変数らをDataFrameに変換
df = DataFrame(data=boston.data, columns=boston.feature_names)
# 目的変数をDataFrameに追加
df['PRICE'] = np.array(boston.target)

# 説明変数は2つ
data = df.loc[:, ['CRIM', 'RM']].values
# 目的変数
target = df.loc[:, 'PRICE'].values

# オブジェクト生成
model = LinearRegression()
# fit関数でパラメータ推定
# dataは2変数なので重回帰分析になる
model.fit(data, target)

# 推定
model.predict([[0.3, 4]])

結果はarray([4.24007956])なので、約 $4,240.

非線形回帰モデル

要点

非線形な構造を持つ現象を捉える。

$$ \hat y = w_0 + w_1 𝚽(x_1) + w_2 𝚽(x_2) + … + w_m 𝚽(x_m) $$

重み$w$については線形: linear-in-parameter

基底展開法

回帰関数として、基底関数と呼ばれる既知の非線形関数とパラメータベクトルの線型結合を使用
未知パラメータは線形回帰モデルと同様に最小二乗法や最尤法により推定
線形回帰と同じように推定可能

よく使われる基底関数

多項式関数
- $𝚽(x)$に$ϕ_j = x^j$を考えると、$\hat y = w_0 + w_1x_i + w_2x_i^2+ \dots + w_mx_i^m$
ガウス型基底関数
- $\displaystyle 𝚽_j(x) = exp{-\frac{(x-μ_j)^2}{2h_j} } $
スプライン関数/Bスプライン関数

未学習(underfitting)と過学習(overfitting)

学習データに対して、十分小さな誤差が得られないモデル->未学習
- 対策: 表現力の高いモデルを利用する
小さな誤差は得られたけど、テスト集合との差が大きいモデル->過学習
- 対策1: 学習データを増やす
- 対策2: 不要な基底関数（変数）を削除して表現力を抑止
- 対策3: 正則化法を利用して表現力を抑止

正則化法（罰則化法）

「モデルの複雑化にしたがって値が大きくなる正則化項（罰則化項）を課した」関数を最小化
形状によって種類がある
- L2ノルム: Ridge推定量
- L1ノルム: Lasso推定量
正則化（平滑化）パラメータ（ハイパーパラメータ）
- モデルの曲線のなめらかさを調節する

$$ S_γ=(\boldsymbol{y}-𝚽\boldsymbol{w})^\top(\boldsymbol{y}-𝚽\boldsymbol{w}) + γR(\boldsymbol{w}) $$

$(\boldsymbol{y}-𝚽\boldsymbol{w})^\top(\boldsymbol{y}-𝚽\boldsymbol{w})$ : 誤差の2乗項
$γR(w)$: 正則化項
$γ$: 正則化パラメータ（$γ>0$）

実装

準備

真の関数を設定する。また、真の関数に数値を代入した後にノイズを加えることで、離散データを作成している。

from pandas import DataFrame
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

#seaborn設定
sns.set()
#背景変更
sns.set_style("darkgrid", {'grid.linestyle': '--'})
#大きさ(スケール変更)
sns.set_context("paper")

n=100

def true_func(x):
    z = 1-48*x+218*x**2-315*x**3+145*x**4
    return z 

def linear_func(x):
    z = x
    return z 

# 真の関数からノイズを伴うデータを生成
# 真の関数からデータ生成
data = np.random.rand(n).astype(np.float32)
data = np.sort(data)
target = true_func(data)

# 　ノイズを加える
noise = 0.5 * np.random.randn(n) 
target = target  + noise

# ノイズ付きデータを描画
plt.scatter(data, target)
plt.title('NonLinear Regression')
plt.legend(loc=2)

非線形回帰モデルの作成

from sklearn.metrics.pairwise import rbf_kernel
from sklearn.linear_model import Ridge

# dataとtargetを2次元1列の行列に変換
data = data.reshape(-1,1)
target = target.reshape(-1,1)

# the radial basis function (RBF): 動径基底関数
# k(x, y) = exp(-γ||x-y||^2)で表される. 
# gammaが大きいほど、細長い釣鐘型になる
# see: https://scikit-learn.org/stable/modules/metrics.html#rbf-kernel
kx = rbf_kernel(X=data, Y=data, gamma=50)

# Ridgeは罰則項付きの残差平方和を最小化する.
# alphaの値が大きいほど罰則が大きくなる
# see: https://scikit-learn.org/stable/modules/linear_model.html#ridge-regression-and-classification
model = Ridge(alpha=30)

# モデルの学習
model.fit(kx, target)

# モデルの予測（学習結果の描画に使う）
p_ridge = model.predict(kx)

# タイトルを描画
plt.title('NonLinear Regression')

# ノイズ付きデータを描画
plt.scatter(data, target, color='blue', label='data')

# RBFカーネルを描画
for i in range(len(kx)):
    plt.plot(data, kx[i], color='black', linestyle='-', linewidth=1, markersize=3, label='rbf', alpha=0.2)

# 非線形回帰モデル（Ridge回帰）を描画
plt.plot(data, p_ridge, color='orange', linestyle='-', linewidth=3, markersize=6, label='ridge')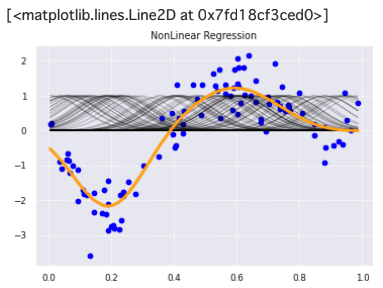

ロジスティック回帰モデル

要点

ロジスティック回帰モデルは分類問題（クラス分類）に用いられる.

識別的アプローチ

$p(C_k| \boldsymbol{x})$を直接モデル化する

識別関数

SVMなどが識別関数に相当する.確率が出せない.

$f(\boldsymbol{x}) > 0 => C=1$
$f(\boldsymbol{x}) < 0 => C=0$

生成的アプローチ

$p(C_k)$とp$(\boldsymbol{x}|C_k)$をモデル化してベイズの定理を用いて$p(C_k|\boldsymbol{x})$を求める $$ \displaystyle p(C_k|\boldsymbol{x}) = \frac{p(C_k, \boldsymbol{x})}{p(\boldsymbol{x})} = \frac{p(\boldsymbol{x}|C_k)p(C_k)}{p(\boldsymbol{x})} $$

$\boldsymbol{x}^\top\boldsymbol{w} ∈ \boldsymbol{R}$なのでsigmoid関数を通して実数全体から0から1の値に変換する.

シグモイド関数の性質

$$ \displaystyle sigmoid(x) = σ(x) = \frac{1}{1+exp(-x)} = \left(1+exp(-x)\right)^{-1} $$

合成関数の微分を使う.

$$ \displaystyle \frac{dσ(x)}{dx} = -1 \times \left(1+exp(-x)\right)^{-2} \times \frac{d(\left(1+exp(-x)\right))}{dx} \times \frac{d(-x)}{dx} \ = -1 \times \left(1+exp(-x)\right)^{-2} \times \left(exp(-x)\right) \times (-1) \ = \frac{1}{1+exp(-x)} \times \frac{1}{1+exp(-x)} \times exp(-x) \ = \frac{1}{1+exp(-x)} \times \frac{exp(-x) }{1+exp(-x)} \ = σ(x) \times (1 - σ(x)) $$

シグモイド関数の微分はシグモイド関数で表せる.

最尤推定

さまざまな分布
- 正規分布、t分布、ガンマ分布、一様分布・・・
- ロジスティック回帰モデルではベルヌーイ分布を利用する
ベルヌーイ分布
- 確率pで1、確率1-pで0をとる、離散確率分布
- 生成されるデータは分布のパラメータによって異なる
- $Y ∼ Be(p)$: ベルヌーイ分布に従う確率変数Y
- $P(y) = p^y(1-p)^{1-y}$: P(0)とP(1)をまとめて表記できる

勾配降下法

$$ \displaystyle Loss: E(\boldsymbol{w})=-\log{L(\boldsymbol{w})} \ = - \sum_{i=1}^{n}{y_i\log{p_i} + (1-y_i)\log{(1-p_i})} $$ $$ \displaystyle p_i = σ(\boldsymbol{w}^\top\boldsymbol{x_i})=\frac{1}{1+\exp(\boldsymbol{w}^\top\boldsymbol{x_i})} $$ $$ z=\boldsymbol{w}^\top\boldsymbol{x_i} $$ 微分のchain ruleを使う. $$ \displaystyle \frac{\partial E(w)}{\partial w} = - \sum_{i=1}^{n} \frac{\partial E_i}{\partial p_i} \times \frac{\partial p_i}{\partial z} \times \frac{\partial z}{\partial w} \ = - \sum_{i=1}^{n}(\frac{y_i}{p_i} - \frac{1 - y_i}{1 - p_i} ) \times p_i(1-p_i) \times x_i \ = - \sum_{i=1}^{n}{(y_i(1-p_i)-p_i(1-y_i)} \times x_i \ = - \sum_{i=1}^{n}(y_i-p_i)x_i $$ $-\log{L(\boldsymbol{w})}$ : 負の対数尤度(negative log-likelihood)

実装

設定

タイタニックの乗客データを利用してロジスティック回帰モデルを作る
特徴量を抽出する

課題

年齢が30歳で男の乗客は生き残れるか

import pandas as pd
from pandas import DataFrame
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LogisticRegression

titanic_df = pd.read_csv('/content/drive/My Drive/rabitchallenge/Stage2/study_ai_ml_google/data/titanic_train.csv')


# 中身をtitanic_df.head(5)等で確認して不要と考えるデータをドロップしておく
titanic_df.drop(['Name', 'Ticket', 'Cabin', 'PassengerId'], axis=1, inplace=True)
# 欠損値を確認
titanic_df[titanic_df.isnull().any(1)].head(10)
# -> AgeにNaNがあることがわかる. 新たな項目として年齢の中央値で補完する
titanic_df['AgeFill'] = titanic_df['Age'].fillna(titanic_df['Age'].mean())
# maleとfemaleを数値にしておく
titanic_df['Gender'] = titanic_df['Sex'].map({'female': 0, 'male': 1}).astype(int)

# 年齢（補完あり）と性別のデータのみ抽出する
data = titanic_df.loc[:, ['AgeFill', 'Gender']].values

# 目的変数である生存フラグのみ抽出する
y = titanic_df.loc[:, ['Survived']].values

model = LogisticRegression()
model.fit(data, y)

model.predict([[30, 1]])
# array([0])
model.predict_proba([[30, 1]])
# array([[0.80668102, 0.19331898]])

年齢が30歳で男の乗客は生き残る確率は19%となった.

主成分分析

要点

多変量データの持つ構造をより少数個の指標に圧縮する.

情報の損失はなるべく小さくしたい
多次元を低次元にすることで可視化ができる

分散が一番大きくなるような軸を見つけると情報の損失が少なくなる。

目的関数: $arg$ $\underset{a ∈ R^m}{max}$ $a_j^\top Var(\overline{X})a_j$
制約条件: $a_j^\top a_j = 1$ （ノルムが1のベクトルという制約）

制約つき最適化問題はラグランジュ関数を最大にする係数ベクトルを求めると良い。目的関数と制約条件が入った関数になっている.

ラグランジュ関数: $E(a_j) = a_j^\top Var(\overline{X})a_j - λ(a_j^\top a_j - 1)$

ラグランジュ関数の微分=0を解く問題は、元データの分散共分散行列の固有値固有ベクトルを解く問題となる。

情報の損失が小さいかどうかは、寄与率の指標で定義する.

寄与率: 第k主成分の分散の、主成分の分散の総和に対する割合
- $\displaystyle c_k= \frac{λ_k}{\sum_{i=1}^{m}λ_i}$
累積寄与率: 第1からk主成分の分散の、主成分の分散の総和に対する割合
- $\displaystyle \gamma_k= \frac{\sum_{j=1}^{k}λ_j}{\sum_{i=1}^{m}λ_i}$

実装

設定

乳がん検査データを利用してロジスティック回帰モデルを作成
主成分を利用して2次元空間に次元圧縮

課題

32次元のデータを2次元上に次元圧縮した際にうまく判別できるかを確認

from google.colab import drive
drive.mount('/content/drive')

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegressionCV
from sklearn.metrics import confusion_matrix
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

cancer_df = pd.read_csv('/content/drive/My Drive/rabitchallenge/Stage2/study_ai_ml_google/data/cancer.csv')
cancer_df.drop('Unnamed: 32', axis=1, inplace=True)

下記でロジスティック回帰を行う

目的変数: diagnosis（B:良性=0, M:悪性=1）
説明変数: radius_mean以降の列

y = cancer_df.diagnosis.apply(lambda a: 1 if a == 'M' else 0)
X = cancer_df.loc[:, 'radius_mean':]

# 学習用とテスト用のデータ分割
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

# データの特徴量のスケールがバラバラなので標準化する
scaler = StandardScaler()
scaler.fit(X_train)
X_train_scaled = scaler.transform(X_train)
# テストデータには訓練データで用いたfitで作成された変換式を使う
X_test_scaled = scaler.transform(X_test)

# ロジスティック回帰で学習
logistic = LogisticRegressionCV(random_state=0)
logistic.fit(X_train_scaled, y_train)

# 検証
print('Train score: {:.3f}'.format(logistic.score(X_train_scaled, y_train)))
print('Test score: {:.3f}'.format(logistic.score(X_test_scaled, y_test)))
# 混合行列の表示
print('Confustion matrix:\n{}'.format(confusion_matrix(y_true=y_test, y_pred=logistic.predict(X_test_scaled))))

訓練スコア: 0.988
検証スコア: 0.972

検証結果

True Negative: 89
False Negative: 3
False Positive: 1
True Positive: 50

次に主成分分析を行う

# PCA
# 30の説明変数がある
pca = PCA(n_components=30)
pca.fit(X_train_scaled)

plt.bar([n for n in range(1, len(pca.explained_variance_ratio_)+1)], pca.explained_variance_ratio_)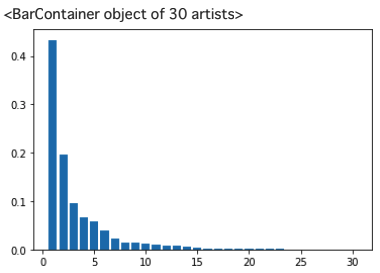

第一主成分の寄与率が約43%, 第二主成分の寄与率が約19%とわかる.第一主成分・第二主成分まで見れば累積寄与率は60パーセントを超える.

# 次元数2まで圧縮
pca = PCA(n_components=2)
X_train_pca = pca.fit_transform(X_train_scaled)

# 散布図にプロット
temp = pd.DataFrame(X_train_pca)
temp['Outcome'] = y_train.values
b = temp[temp['Outcome'] == 0]
m = temp[temp['Outcome'] == 1]
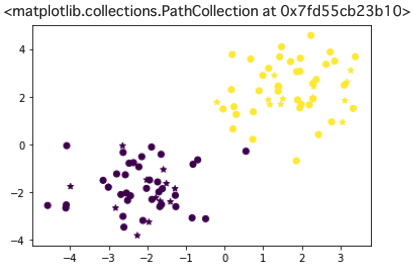
plt.scatter(x=b[0], y=b[1], marker='o') # 良性は○でマーク
plt.scatter(x=m[0], y=m[1], marker='^') # 悪性は△でマーク
plt.xlabel('PC 1') # 第1主成分をx軸
plt.ylabel('PC 2') # 第2主成分をy軸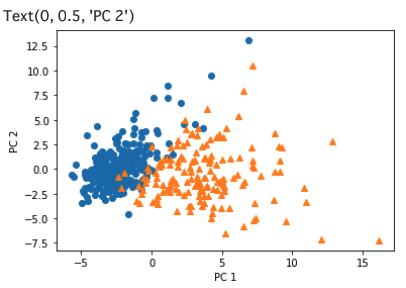

30次元から2次元に落としても、丸い青の点と三角のオレンジの点が少し混ざっているところがあるものの、境界線が引けそうな分布に分かれている.

サポートベクターマシン

要点

サポートベクターマシンは、分類タスクに主に使われる.
サポートベクトルとは、分類境界の決定に関わる分類境界に最も近いデータ$x_i$のこと.
決定関数$f(x) = w^\top x + b$
- $w,x$は同次元のベクトルで、$w^\top x $は内積を表す
- $y = sgn f(x) = \begin{cases} ~ +1 ~ (f(x) > 0) \\ -1 ~ (f(x) < 0) \end{cases}$ ※sgnは符号関数
- f(x) = 0が分類境界となる

線形サポートベクトル分類（ハードマージン）

分類可能性を仮定した場合のSV分類のことをハードマージンと呼ぶ.
分類境界を挟んで2つのクラスがどれくらい離れているかをマージンと呼ぶ。
マージンが大きいほど良い分類境界になるため、大きなマージンを持つ分類境界を探す（マージン最大化）
- 分類境界$f(x)=0$と分類境界から最も近くにあるデータ$x_i$との距離を最大化することと等しい

$$ \underset{w, b}{max} \left[ \underset{i}{min} \frac{f(x_i)}{||w||} \right] = \underset{w, b}{max} \left[ \underset{i}{min} \frac{|w^\top x_i + b|}{||w||} \right] = \underset{w, b}{max} \left[ \underset{i}{min} \frac{y_i[w^\top x_i + b]}{||w||} \right] ≡ \underset{w, b}{max} \frac{M(w, b)}{||w||} $$

$w, b$を規格化して整理すると、下記のような最適化問題になる.

$$ \underset{w, b}{min} \frac{1}{2} {||w||^2}, ~ y_i[w^\top x_i+b] ≥ 1 ~ (i = 1, \dots, n) $$

線形サポートベクトル分類（ソフトマージン)

分類可能でないデータに適用できるように拡張したものをソフトマージンと呼ぶ.
マージン内に入るデータの誤差をあらわす変数$\xi$(スラック変数）を導入して下記のような最適化問題に帰着させる

$$ \underset{w, b, \xi}{min} \left[ \frac{1}{2} {||w||^2} + C \sum_{i=1}^n \xi_i \right], ~ y_i[w^\top x_i+b] ≥ 1-\xi_i, ~ \xi_i \ge 0 ~ (i = 1, \dots, n) $$

SV分類の先述の主問題と等価な双対問題を解くことで計算量を減らしている.
非線形分離をする時に、データを高次元に拡張して、カーネルトリックを利用して計算量を減らしてその高次元空間で線形問題として分類問題を解くことができる.

実装

線形分離可能なデータの分類.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split

# ２値分類したデータを生成する関数
def gen_data():
    x0 = np.random.normal(size=100).reshape(-1, 2) - 2.
    x1 = np.random.normal(size=100).reshape(-1, 2) + 2.
    X = np.concatenate([x0, x1])
    y = np.concatenate([np.zeros(50), np.ones(50)]).astype(int)
    return X, y

X, y = gen_data()
# 訓練データと検証データに分類
x_train, x_test, y_train, y_test = train_test_split(X, y, random_state=0)

# サポートベクター分類の線形カーネルを使う
svc = SVC(kernel='linear')

# 学習
svc.fit(x_train, y_train)

# 予測
y_pred = svc.predict(x_test)

plt.scatter(x_train[:, 0], x_train[:, 1], c=y_train)
plt.scatter(x_test[:, 0], x_test[:, 1], c=y_pred, marker="*")

機械学習 - ラビット・チャレンジ レポート

線形回帰モデル

要点

回帰問題

線形回帰モデル

説明変数が1次元の場合

説明変数が多次元の場合

留意点

二乗誤差

実装

設定

課題

非線形回帰モデル

要点

基底展開法

よく使われる基底関数

未学習(underfitting)と過学習(overfitting)

正則化法（罰則化法）

実装

準備

非線形回帰モデルの作成

ロジスティック回帰モデル

要点

識別的アプローチ

識別関数

生成的アプローチ

シグモイド関数の性質

最尤推定

勾配降下法

実装

設定

課題

主成分分析

要点

実装

設定

課題

サポートベクターマシン

要点

線形サポートベクトル分類（ハードマージン）

線形サポートベクトル分類（ソフトマージン)

実装

関連記事

ラビット・チャレンジを受講した感想・まとめ

深層学習day4 - ラビット・チャレンジ レポート

深層学習day3 - ラビット・チャレンジ レポート

深層学習day2 - ラビット・チャレンジ レポート

深層学習day1 - ラビット・チャレンジ レポート

応用数学 - ラビット・チャレンジ レポート

機械学習 - ラビット・チャレンジレポート

深層学習day4 - ラビット・チャレンジレポート

深層学習day3 - ラビット・チャレンジレポート

深層学習day2 - ラビット・チャレンジレポート

深層学習day1 - ラビット・チャレンジレポート

応用数学 - ラビット・チャレンジレポート