Section1：勾配消失問題

1-1 要点

誤差逆伝播法で重みを更新するとき、微分連鎖率によって更新していく。 中間層の活性化関数としてシグモイド関数を使うと、微分すると高々0.25のため、層が多くなるにつれて高々0.25の掛け算が何度も行われてしまい、更新がされなくなってしまう。更新ができなくなってしまうことが勾配消失問題である。

消失問題の解決法として以下がある.

• 活性化関数の選択
• 重みの初期設定
• バッチ正規化

1-1-1 活性化関数の選択

ReLU関数を使う.

$$ \displaystyle f(x) = \begin{cases} ~ x ~ (x > 0) \\ 0 ~ (x \leqq 0) \end{cases} $$

微分すると0か1になるためメリットがある

• 活性化関数の微分による勾配消失がなくなる
• 重みがスパース化される

1-1-2 重みの初期化設定

• Xavierの初期値
  • 前のノード数nの時、平均0, 分散$\frac{1}{\sqrt{n}}$の分布として重みを初期化する
  • S字型の関数に有効
• Heの初期化
  • 前のノード数nの時、平均0, 分散$\sqrt{\frac{2}{n}}$の分布として重みを初期化する
  • ReLU関数に有効

1-1-3 バッチ正規化

バッチ正規化は、ミニバッチ単位で入力データの偏りを抑制する手法.バッチ正規化の手順は以下のとおり.

1. ミニバッチの平均を求める
2. ミニバッチの分散を求める
3. ミニバッチの正規化をする: $\hat {x}_{ni}$
4. 変倍・移動する: $y_{ni}=γx_{ni}+β$
   • $γ$: スケーリングパラメータ
   • $β$: シフトパラメータ

1-2 実装

google colabの準備

import sys
import os
ENV_COLAB = True  if 'google.colab' in sys.modules else False 

# google drive のマウント
if ENV_COLAB:
  from google.colab import drive 
  drive.mount('/content/drive')
  os.chdir('/content/drive/My Drive/rabitchallenge/Stage3/day2/DNN_code_colab_day2/notebook')

sys.path.append(os.pardir)

ニューラルネットワークを定義したクラスを読み込む

import numpy as np
from common import layers
from collections import OrderedDict
from common import functions
from data.mnist import load_mnist
import matplotlib.pyplot as plt

class MultiLayerNet:
    '''
    input_size: 入力層のノード数
    hidden_size_list: 隠れ層のノード数のリスト
    output_size: 出力層のノード数
    activation: 活性化関数
    weight_init_std: 重みの初期化方法
    '''
    def __init__(self, input_size, hidden_size_list, output_size, activation='relu', weight_init_std='relu'):
        self.input_size = input_size
        self.output_size = output_size
        self.hidden_size_list = hidden_size_list
        self.hidden_layer_num = len(hidden_size_list)
        self.params = {}

        # 重みの初期化
        self.__init_weight(weight_init_std)

        # レイヤの生成, sigmoidとreluのみ扱う
        activation_layer = {'sigmoid': layers.Sigmoid, 'relu': layers.Relu}
        self.layers = OrderedDict() # 追加した順番に格納
        for idx in range(1, self.hidden_layer_num+1):
            self.layers['Affine' + str(idx)] = layers.Affine(self.params['W' + str(idx)], self.params['b' + str(idx)])
            self.layers['Activation_function' + str(idx)] = activation_layer[activation]()

        idx = self.hidden_layer_num + 1
        self.layers['Affine' + str(idx)] = layers.Affine(self.params['W' + str(idx)], self.params['b' + str(idx)])

        self.last_layer = layers.SoftmaxWithLoss()

    def __init_weight(self, weight_init_std):
        all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size]
        for idx in range(1, len(all_size_list)):
            scale = weight_init_std
            if str(weight_init_std).lower() in ('relu', 'he'):
                scale = np.sqrt(2.0 / all_size_list[idx - 1])
            elif str(weight_init_std).lower() in ('sigmoid', 'xavier'):
                scale = np.sqrt(1.0 / all_size_list[idx - 1])

            self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx])
            self.params['b' + str(idx)] = np.zeros(all_size_list[idx])

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)

        return x

    def loss(self, x, d):
        y = self.predict(x)

        weight_decay = 0
        for idx in range(1, self.hidden_layer_num + 2):
            W = self.params['W' + str(idx)]

        return self.last_layer.forward(y, d) + weight_decay

    def accuracy(self, x, d):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if d.ndim != 1 : d = np.argmax(d, axis=1)

        accuracy = np.sum(y == d) / float(x.shape[0])
        return accuracy

    def gradient(self, x, d):
        # forward
        self.loss(x, d)

        # backward
        dout = 1
        dout = self.last_layer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        # 設定
        grad = {}
        for idx in range(1, self.hidden_layer_num+2):
            grad['W' + str(idx)] = self.layers['Affine' + str(idx)].dW
            grad['b' + str(idx)] = self.layers['Affine' + str(idx)].db

        return grad

ReLU関数とHe初期化を実行する

# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)

print("データ読み込み完了")

network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='relu', weight_init_std='He')

iters_num = 2000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.1

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]

    # 勾配
    grad = network.gradient(x_batch, d_batch)
    
    for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
        network.params[key] -= learning_rate * grad[key]
    
    loss = network.loss(x_batch, d_batch)
    train_loss_list.append(loss)
    
    if (i + 1) % plot_interval == 0:
        accr_test = network.accuracy(x_test, d_test)
        accuracies_test.append(accr_test)        
        accr_train = network.accuracy(x_batch, d_batch)
        accuracies_train.append(accr_train)
        
        # print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        # print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
        

lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()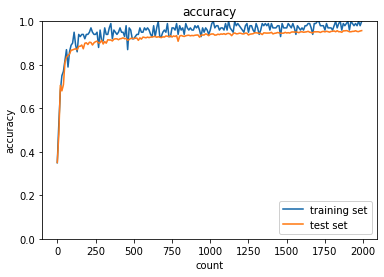

勾配消失が起きずにイテレーション回数が250回ほどで正答率は90％近くになっている.

勾配消失を置きにくくするために以下を実施している.

• 活性化関数をReLUにしたこと
• 重み初期化にHeの初期化を使っていること

Section2 : 学習率最適化手法

2-1 要点

• 学習率最適化手法
  • モメンタム
  • AdaGrad
  • RMSProp
  • Adam

学習率が固定の場合

• 学習率が大きすぎると、最適値に辿り着かずに発散する.
• 学習率が小さすぎると、
  • 収束するまでに時間がかかる
  • 大域局所最適値に収束しづらくなる

学習率最適化の指針

• 初期の学習率は大きくして、徐々に小さくしていく
• パラメータごとに学習率を可変させる

勾配降下法

$$ w^{t+1} = w^t - ε∇E $$

モメンタム

慣性を導入する.
$$ V_t = μV_{t-1}-ε∇E \ w^{t+1} = w^t + V_t $$

• 慣性: $μ$ ハイパーパラメータ
• 学習率: $ε$

AdaGrad

$$ h_0 = θ \ h_t = h_{t-1}-(∇E)^2 \ w^{t+1} = w^t -ε \frac{1}{\sqrt h_t + θ}∇E $$

• $h$: これまでの学習の値を溜め込んでいる.経験のようなもの.
• $θ$: 適当な値

RMSProp

AdaGradの鞍点問題を解消する試み。 $$ h_t=αh_{t-1} + (1-α）(∇E)^2 \ w^{t+1} =w^t -ε \frac{1}{\sqrt h_t + θ}∇E $$

• α: ハイパーパラメータ. αがhにかかっている->前回の学習の値をどれだけ使うかを意味する.

Adam

モメンタムとRMSPropのメリットをあわせもつ改良版.

2-2 実装

from multi_layer_net import MultiLayerNet

# データの読み込み
(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True, one_hot_label=True)

print("データ読み込み完了")

# batch_normalizationの設定 ================================
use_batchnorm = False
# ====================================================

network = MultiLayerNet(input_size=784, hidden_size_list=[40, 20], output_size=10, activation='sigmoid', weight_init_std=0.01,
                       use_batchnorm=use_batchnorm)

iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
decay_rate = 0.99

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]

    # 勾配
    grad = network.gradient(x_batch, d_batch)
    if i == 0:
        h = {}
    for key in ('W1', 'W2', 'W3', 'b1', 'b2', 'b3'):
        if i == 0:
            h[key] = np.zeros_like(network.params[key])
        h[key] *= decay_rate  # <- 数式のαがdecay_rateに相当する
        h[key] += (1 - decay_rate) * np.square(grad[key])
        network.params[key] -= learning_rate * grad[key] / (np.sqrt(h[key]) + 1e-7)  # <- RMSPropの式の通り、各重み、バイアスを再計算している

        loss = network.loss(x_batch, d_batch)
        train_loss_list.append(loss)                
        
    if (i + 1) % plot_interval == 0:
        accr_test = network.accuracy(x_test, d_test)
        accuracies_test.append(accr_test)        
        accr_train = network.accuracy(x_batch, d_batch)
        accuracies_train.append(accr_train)
        
        # print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        # print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))
        
        
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()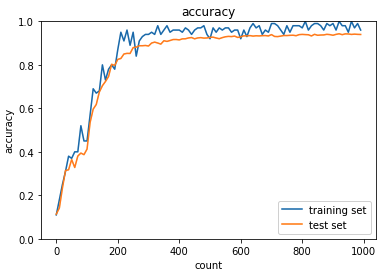

学習ごとにhを計算して学習率を変えていくRMSPropを使って学習が進んでいることが確認できた.

Section3 : 過学習

3-1 要点

過学習が発生すると、訓練データに対して正答率が上がっていき、汎化性能を持たなくなってしまう.テスト誤差と訓練誤差とで学習曲線が乖離するのでグラフを作成すると過学習が認識しやすい.

入力データが少ないわりに、ニューラルネットワークの自由度が高いと過学習しやすい

正則化

ネットワークの自由度（層数、ノード数、パラメータ数など）を制約すること.

• L1正則化、L2正則化
  • $ p = 1$の場合、L1正則化という. （マンハッタン距離）
  • $ p = 2$の場合、L2正則化という. （ユーグリッド距離）

$$ \displaystyle E_n(w) + \frac{1}{p} λ\ ||\ x\ ||_p $$

• ドロップアウト
  • ランダムにノードを削除して学習させること

3-2 実装

ドロップアウトとL1正則化

(x_train, d_train), (x_test, d_test) = load_mnist(normalize=True)

print("データ読み込み完了")

# 過学習を再現するために、学習データを削減
x_train = x_train[:300]
d_train = d_train[:300]

# ドロップアウト設定 ======================================
use_dropout = True
dropout_ratio = 0.08
# ====================================================

network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10,
                        use_dropout = use_dropout, dropout_ratio = dropout_ratio)  # <- dropoutの情報をクラスのコンストラクタで処理している

iters_num = 1000
train_size = x_train.shape[0]
batch_size = 100
learning_rate=0.01

train_loss_list = []
accuracies_train = []
accuracies_test = []
hidden_layer_num = network.hidden_layer_num

plot_interval=10

# 正則化強度設定 ======================================
weight_decay_lambda=0.004
# =================================================

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]

    grad = network.gradient(x_batch, d_batch)
    weight_decay = 0
    
    for idx in range(1, hidden_layer_num+1):
        grad['W' + str(idx)] = network.layers['Affine' + str(idx)].dW + weight_decay_lambda * np.sign(network.params['W' + str(idx)])
        grad['b' + str(idx)] = network.layers['Affine' + str(idx)].db
        network.params['W' + str(idx)] -= learning_rate * grad['W' + str(idx)]
        network.params['b' + str(idx)] -= learning_rate * grad['b' + str(idx)]        
        weight_decay += weight_decay_lambda * np.sum(np.abs(network.params['W' + str(idx)]))  # <- L1正則化が行われている

    loss = network.loss(x_batch, d_batch) + weight_decay
    train_loss_list.append(loss)        
        
    if (i+1) % plot_interval == 0:
        accr_train = network.accuracy(x_train, d_train)
        accr_test = network.accuracy(x_test, d_test)
        accuracies_train.append(accr_train)
        accuracies_test.append(accr_test)
        
        # print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        # print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))               
        
lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()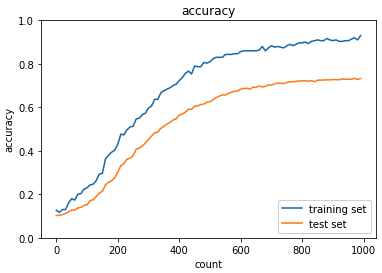

ドロップアウトとL1正則化を使って学習をおこなっている. 訓練データの正答率はL1正則化の影響で100%にはならない. 検証データに対する正答率も学習のイテレーションを重ねるにつれて上がっていることがわかる.

Section4 : 畳み込みニューラルネットワークの概念

4-1 要点

CNNでは次元間でつながりのあるデータを扱える

畳み込み層

フィルターを用いて次元の繋がりを保ったまま学習することができる.

フィルター（＝全結合層でいう重み） = 入力データをみるひとの個性として振る舞う。

• バイアス
  • 入力画像をフィルターを通して出力されたものにバイアスを加算する
• パディング
  • 入力画像の全方向にパディングをするとフィルターを通しても、入力画像と出力画像の大きさを揃えることができる
• ストライド
  • フィルターのずらす大きさを決める
  • ストライドが大きいと出力の画像サイズを小さくなる
• チャンネル
  • フィルターを何個も使う

プーリング層

マスの中で最大値や平均を出力の値として採用する

4-2 実装

畳み込み層

class Convolution:
    # W: フィルター, b: バイアス
    def __init__(self, W, b, stride=1, pad=0):
        self.W = W
        self.b = b
        self.stride = stride
        self.pad = pad
        
        # 中間データ（backward時に使用）
        self.x = None   
        self.col = None
        self.col_W = None
        
        # フィルター・バイアスパラメータの勾配
        self.dW = None
        self.db = None

    def forward(self, x):
        # FN: filter_number, C: channel, FH: filter_height, FW: filter_width
        FN, C, FH, FW = self.W.shape
        N, C, H, W = x.shape
        # 出力値のheight, width
        out_h = 1 + int((H + 2 * self.pad - FH) / self.stride)
        out_w = 1 + int((W + 2 * self.pad - FW) / self.stride)
        
        # xを行列に変換
        col = im2col(x, FH, FW, self.stride, self.pad)  # <- im2col関数は定義しておく必要がある. レポート上は割愛する.
        # フィルターをxに合わせた行列に変換
        col_W = self.W.reshape(FN, -1).T

        out = np.dot(col, col_W) + self.b  # <- np.dotで内積計算しやすい形にcolは整形されている
        # 計算のために変えた形式を戻す
        out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)

        self.x = x
        self.col = col
        self.col_W = col_W

        return out

    def backward(self, dout):
        FN, C, FH, FW = self.W.shape
        dout = dout.transpose(0, 2, 3, 1).reshape(-1, FN)

        self.db = np.sum(dout, axis=0)
        self.dW = np.dot(self.col.T, dout)
        self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)

        dcol = np.dot(dout, self.col_W.T)
        # dcolを画像データに変換
        dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad) # <- col2im関数は定義しておく必要がある. レポート上は割愛する.

        return dx

プーリング層

class Pooling:
    def __init__(self, pool_h, pool_w, stride=1, pad=0):
        self.pool_h = pool_h
        self.pool_w = pool_w
        self.stride = stride
        self.pad = pad
        
        self.x = None
        self.arg_max = None

    def forward(self, x):
        N, C, H, W = x.shape
        out_h = int(1 + (H - self.pool_h) / self.stride)
        out_w = int(1 + (W - self.pool_w) / self.stride)
        
        # xを行列に変換
        col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)  # <- col2im関数は定義しておく必要がある. レポート上は割愛する.
        # プーリングのサイズに合わせてリサイズ
        col = col.reshape(-1, self.pool_h*self.pool_w)  # <- リサイズすることで行ごとのargmax計算を容易にしている
        
        # 行ごとに最大値を求める
        arg_max = np.argmax(col, axis=1)
        out = np.max(col, axis=1)
        # 整形
        out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)

        self.x = x
        self.arg_max = arg_max

        return out

    def backward(self, dout):
        dout = dout.transpose(0, 2, 3, 1)
        
        pool_size = self.pool_h * self.pool_w
        dmax = np.zeros((dout.size, pool_size))
        dmax[np.arange(self.arg_max.size), self.arg_max.flatten()] = dout.flatten()
        dmax = dmax.reshape(dout.shape + (pool_size,)) 
        
        dcol = dmax.reshape(dmax.shape[0] * dmax.shape[1] * dmax.shape[2], -1)
        dx = col2im(dcol, self.x.shape, self.pool_h, self.pool_w, self.stride, self.pad)  # <- im2col関数は定義しておく必要がある. レポート上は割愛する.
        
        return dx

Section5 : 最新のCNN

5-1 要点

AlexNet

• 5層の畳み込み層とプーリング層、それに続く３層の全結合層から構成される
• 過学習を防ぐために全結合層にドロップアウトを使用している

---

• 全結合層への移行方法
  • Fratten: 全てのデータを一列に並べる（初期のNNでよく使われる）
  • GlobalMaxPooling: 各チャンネルの一番最大の値を使って一列にデータを並べる
  • GlobalAvgPooling: 各チャンネルの平均の値を使って一列にデータを並べる

5-2 実装

import pickle
import numpy as np
from collections import OrderedDict
from common import layers
from data.mnist import load_mnist
import matplotlib.pyplot as plt
from common import optimizer

class DeepConvNet:
    '''
    認識率99%以上の高精度なConvNet

    conv - relu - conv- relu - pool -
    conv - relu - conv- relu - pool -
    conv - relu - conv- relu - pool -
    affine - relu - dropout - affine - dropout - softmax
    '''
    def __init__(self, input_dim=(1, 28, 28),
                 conv_param_1 = {'filter_num':16, 'filter_size':3, 'pad':1, 'stride':1},
                 conv_param_2 = {'filter_num':16, 'filter_size':3, 'pad':1, 'stride':1},
                 conv_param_3 = {'filter_num':32, 'filter_size':3, 'pad':1, 'stride':1},
                 conv_param_4 = {'filter_num':32, 'filter_size':3, 'pad':2, 'stride':1},
                 conv_param_5 = {'filter_num':64, 'filter_size':3, 'pad':1, 'stride':1},
                 conv_param_6 = {'filter_num':64, 'filter_size':3, 'pad':1, 'stride':1},
                 hidden_size=50, output_size=10):
        # 重みの初期化===========
        # 各層のニューロンひとつあたりが、前層のニューロンといくつのつながりがあるか
        pre_node_nums = np.array([1*3*3, 16*3*3, 16*3*3, 32*3*3, 32*3*3, 64*3*3, 64*4*4, hidden_size])
        wight_init_scales = np.sqrt(2.0 / pre_node_nums)  # Heの初期値
        
        self.params = {}
        pre_channel_num = input_dim[0]
        for idx, conv_param in enumerate([conv_param_1, conv_param_2, conv_param_3, conv_param_4, conv_param_5, conv_param_6]):
            self.params['W' + str(idx+1)] = wight_init_scales[idx] * np.random.randn(conv_param['filter_num'], pre_channel_num, conv_param['filter_size'], conv_param['filter_size'])
            self.params['b' + str(idx+1)] = np.zeros(conv_param['filter_num'])
            pre_channel_num = conv_param['filter_num']
        self.params['W7'] = wight_init_scales[6] * np.random.randn(pre_node_nums[6], hidden_size)
        print(self.params['W7'].shape)
        self.params['b7'] = np.zeros(hidden_size)
        self.params['W8'] = wight_init_scales[7] * np.random.randn(pre_node_nums[7], output_size)
        self.params['b8'] = np.zeros(output_size)

        # レイヤの生成===========
        self.layers = []
        self.layers.append(layers.Convolution(self.params['W1'], self.params['b1'], 
                           conv_param_1['stride'], conv_param_1['pad']))
        self.layers.append(layers.Relu())
        self.layers.append(layers.Convolution(self.params['W2'], self.params['b2'], 
                           conv_param_2['stride'], conv_param_2['pad']))
        self.layers.append(layers.Relu())
        self.layers.append(layers.Pooling(pool_h=2, pool_w=2, stride=2))
        self.layers.append(layers.Convolution(self.params['W3'], self.params['b3'], 
                           conv_param_3['stride'], conv_param_3['pad']))
        self.layers.append(layers.Relu())
        self.layers.append(layers.Convolution(self.params['W4'], self.params['b4'],
                           conv_param_4['stride'], conv_param_4['pad']))
        self.layers.append(layers.Relu())
        self.layers.append(layers.Pooling(pool_h=2, pool_w=2, stride=2))
        self.layers.append(layers.Convolution(self.params['W5'], self.params['b5'],
                           conv_param_5['stride'], conv_param_5['pad']))
        self.layers.append(layers.Relu())
        self.layers.append(layers.Convolution(self.params['W6'], self.params['b6'],
                           conv_param_6['stride'], conv_param_6['pad']))
        self.layers.append(layers.Relu())
        self.layers.append(layers.Pooling(pool_h=2, pool_w=2, stride=2))
        self.layers.append(layers.Affine(self.params['W7'], self.params['b7']))
        self.layers.append(layers.Relu())
        self.layers.append(layers.Dropout(0.5))
        self.layers.append(layers.Affine(self.params['W8'], self.params['b8']))
        self.layers.append(layers.Dropout(0.5))
        
        self.last_layer = layers.SoftmaxWithLoss()

    def predict(self, x, train_flg=False):
        for layer in self.layers:
            if isinstance(layer, layers.Dropout):
                x = layer.forward(x, train_flg)
            else:
                x = layer.forward(x)
        return x

    def loss(self, x, d):
        y = self.predict(x, train_flg=True)
        return self.last_layer.forward(y, d)

    def accuracy(self, x, d, batch_size=100):
        if d.ndim != 1 : d = np.argmax(d, axis=1)

        acc = 0.0

        for i in range(int(x.shape[0] / batch_size)):
            tx = x[i*batch_size:(i+1)*batch_size]
            td = d[i*batch_size:(i+1)*batch_size]
            y = self.predict(tx, train_flg=False)
            y = np.argmax(y, axis=1)
            acc += np.sum(y == td)

        return acc / x.shape[0]

    def gradient(self, x, d):
        # forward
        self.loss(x, d)

        # backward
        dout = 1
        dout = self.last_layer.backward(dout)

        tmp_layers = self.layers.copy()
        tmp_layers.reverse()
        for layer in tmp_layers:
            dout = layer.backward(dout)

        # 設定
        grads = {}
        for i, layer_idx in enumerate((0, 2, 5, 7, 10, 12, 15, 18)):
            grads['W' + str(i+1)] = self.layers[layer_idx].dW
            grads['b' + str(i+1)] = self.layers[layer_idx].db

        return grads

(x_train, d_train), (x_test, d_test) = load_mnist(flatten=False)

# 処理に時間のかかる場合はデータを削減 
x_train, d_train = x_train[:500], d_train[:500]  # <- 時間がかかるのでデータを削減した
x_test, d_test = x_test[:100], d_test[:100]  # <- 時間がかかるのでデータを削減した

print("データ読み込み完了")

network = DeepConvNet()  
optimizer = optimizer.Adam()

iters_num = 300 # <- 時間がかかるのでイテレーションを減らした
train_size = x_train.shape[0]
batch_size = 10

train_loss_list = []
accuracies_train = []
accuracies_test = []

plot_interval=10

for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    d_batch = d_train[batch_mask]
    
    grad = network.gradient(x_batch, d_batch)
    optimizer.update(network.params, grad)

    loss = network.loss(x_batch, d_batch)
    train_loss_list.append(loss)

    if (i+1) % plot_interval == 0:
        accr_train = network.accuracy(x_train, d_train)
        accr_test = network.accuracy(x_test, d_test)
        accuracies_train.append(accr_train)
        accuracies_test.append(accr_test)        

        # print('Generation: ' + str(i+1) + '. 正答率(トレーニング) = ' + str(accr_train))
        # print('                : ' + str(i+1) + '. 正答率(テスト) = ' + str(accr_test))

lists = range(0, iters_num, plot_interval)
plt.plot(lists, accuracies_train, label="training set")
plt.plot(lists, accuracies_test,  label="test set")
plt.legend(loc="lower right")
plt.title("accuracy")
plt.xlabel("count")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
# グラフの表示
plt.show()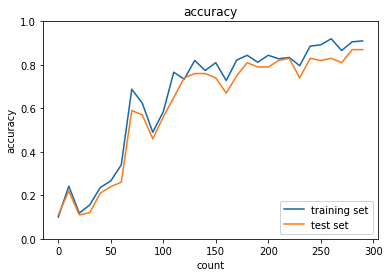

正答率が上がっていくことが確認できた。学習のイテレーションをさらに重ねればより精度の高いモデルができそうである.

畳み込み層やプーリング層、活性化層などレイヤーがおおいと、パラメータ更新をする学習に時間がかかってしまうため、学習させるデータ数の削減を行った.

[フレームワーク演習] 正則化/最適化

6-1 要点

過学習を抑制する方法

• （パラメータ）正則化: ネットワークの自由度を制約(Regularization）すること.
  • L1正則化(Lasso回帰): パラメータの発散抑制.
  • L2正則化(Ridge回帰): パラメータ自体の削減.
  • Elastic Net: L1、L2正則化を組み合わせたもの.
• 正則化レイヤー
  • Dropout
• 正規化レイヤー
  • Batch正規化
  • Layer正規化
  • Instance正規化

6-2 実装

tensorflow.kerasを使用した実装.

# モジュールのロード
import tensorflow as tf
import numpy as np

# データのロード
(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()

x_train = x_train / 255
x_test = x_test / 255
y_train = tf.one_hot(y_train.reshape(len(y_train)), depth=10)
y_test = tf.one_hot(y_test.reshape(len(y_test)), depth=10)

print(x_train.shape)
print(y_train.shape)
print(x_test.shape)
print(y_test.shape)

# 画像のラベル
index2label = {
    0: 'airplane',
    1: 'automobile',
    2: 'bird',
    3: 'cat',
    4: 'deer',
    5: 'dog',
    6: 'frog',
    7: 'horse',
    8: 'ship',
    9: 'truck'
}

# 出力結果
Downloading data from https://www.cs.toronto.edu/~kriz/cifar-10-python.tar.gz
170500096/170498071 [==============================] - 4s 0us/step
170508288/170498071 [==============================] - 4s 0us/step
(50000, 32, 32, 3)
(50000, 10)
(10000, 32, 32, 3)
(10000, 10)

import matplotlib.pyplot as plt
import random

index = 0
count = 50

plt.figure(figsize=(16, 10))

for i, img in enumerate(x_test[index:index+count]):
    plt.subplot(5, 10, i + 1)
    plt.imshow(img)
    plt.axis('off')
    plt.title(index2label[np.argmax(y_test[i])])

plt.show()

epochs = 5
batch_size = 256

# 畳み込み層とプーリング層があるモデルを作成している.
def create_model(input_shape, class_num):
    model = tf.keras.models.Sequential([
        tf.keras.layers.Conv2D(32, 3, padding='same', input_shape=input_shape[1:], activation='relu'),
        tf.keras.layers.Conv2D(32, 3, activation='relu'),
        tf.keras.layers.MaxPooling2D(),
        tf.keras.layers.Flatten(),
        tf.keras.layers.Dense(512, activation='relu', activity_regularizer=tf.keras.regularizers.L1(0.01)),  # <- ここにL1正則化を設定している
        tf.keras.layers.Dense(class_num, activation='softmax'),
    ])

    model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['acc'])

    return model

model = create_model(x_train.shape, 10)
model.summary()

# 出力結果
Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 conv2d (Conv2D)             (None, 32, 32, 32)        896       
                                                                 
 conv2d_1 (Conv2D)           (None, 30, 30, 32)        9248      
                                                                 
 max_pooling2d (MaxPooling2D  (None, 15, 15, 32)       0         
 )                                                               
                                                                 
 flatten (Flatten)           (None, 7200)              0         
                                                                 
 dense (Dense)               (None, 512)               3686912   
                                                                 
 dense_1 (Dense)             (None, 10)                5130      
                                                                 
=================================================================
Total params: 3,702,186
Trainable params: 3,702,186
Non-trainable params: 0
_________________________________________________________________

history = model.fit(x_train, y_train, 
                    validation_data=(x_test, y_test),
                    batch_size=batch_size, epochs=epochs)

# 出力結果
Epoch 1/5
196/196 [==============================] - 133s 670ms/step - loss: 1.8654 - acc: 0.3811 - val_loss: 1.5788 - val_acc: 0.4943
Epoch 2/5
196/196 [==============================] - 131s 669ms/step - loss: 1.4655 - acc: 0.5326 - val_loss: 1.3722 - val_acc: 0.5688
Epoch 3/5
196/196 [==============================] - 126s 645ms/step - loss: 1.2765 - acc: 0.6007 - val_loss: 1.2312 - val_acc: 0.6180
Epoch 4/5
196/196 [==============================] - 126s 643ms/step - loss: 1.1483 - acc: 0.6486 - val_loss: 1.1743 - val_acc: 0.6445
Epoch 5/5
196/196 [==============================] - 132s 671ms/step - loss: 1.0592 - acc: 0.6796 - val_loss: 1.1291 - val_acc: 0.6465

フレームワークを使うと、モデルの構築や確認、学習、進捗確認など簡単に実装ができる. 簡単に実装ができてしまうため、自分が想像したモデルなのかよく理解して使う必要がある.